Win your fantasy league using operations research

July 15, 2024 · 22 mins · 3963 words

I’ve never been good at playing football ¹. I started playing again last year and I have scored more own goals than goals for my team. Also, I support the RCD Espanyol ², which has spent last season in the second division and has miraculously ascended to the first division last week. And to be honest, I only watch games to spend time with my friends and family. So it’s not a secret that I’m not a football expert, and I have no shame in admitting it. But I’m very competitive. So when my friends invited me to a football fantasy league ³ some years ago I said “yes, and I’m going to wipe the floor with you, losers!”.

Fantasy and knapsacks

Since I’m not a football expert, and I only know the names of a couple of players, I needed another strategy to win my friends. In our league ⁴ we have a fixed budget and we have to select 11 players that will compete during the next set of games. Usually, better players -ie: players that score more points- are more expensive than worse players. But there are always exceptions. For example, Bellingham (one of the Ballon d’Or candidates) costs 64M, but Carvajal (one of the few players with 6 Champions League) only costs 10M. The strategy is then to select cheap players that score a lot of points.

After thinking about the problem for a while it started to ring a bell. We have a maximum budget per team. Each player has a cost. Each player has a value. We want to maximize the value of the team. Isn’t this just the knapsack problem?

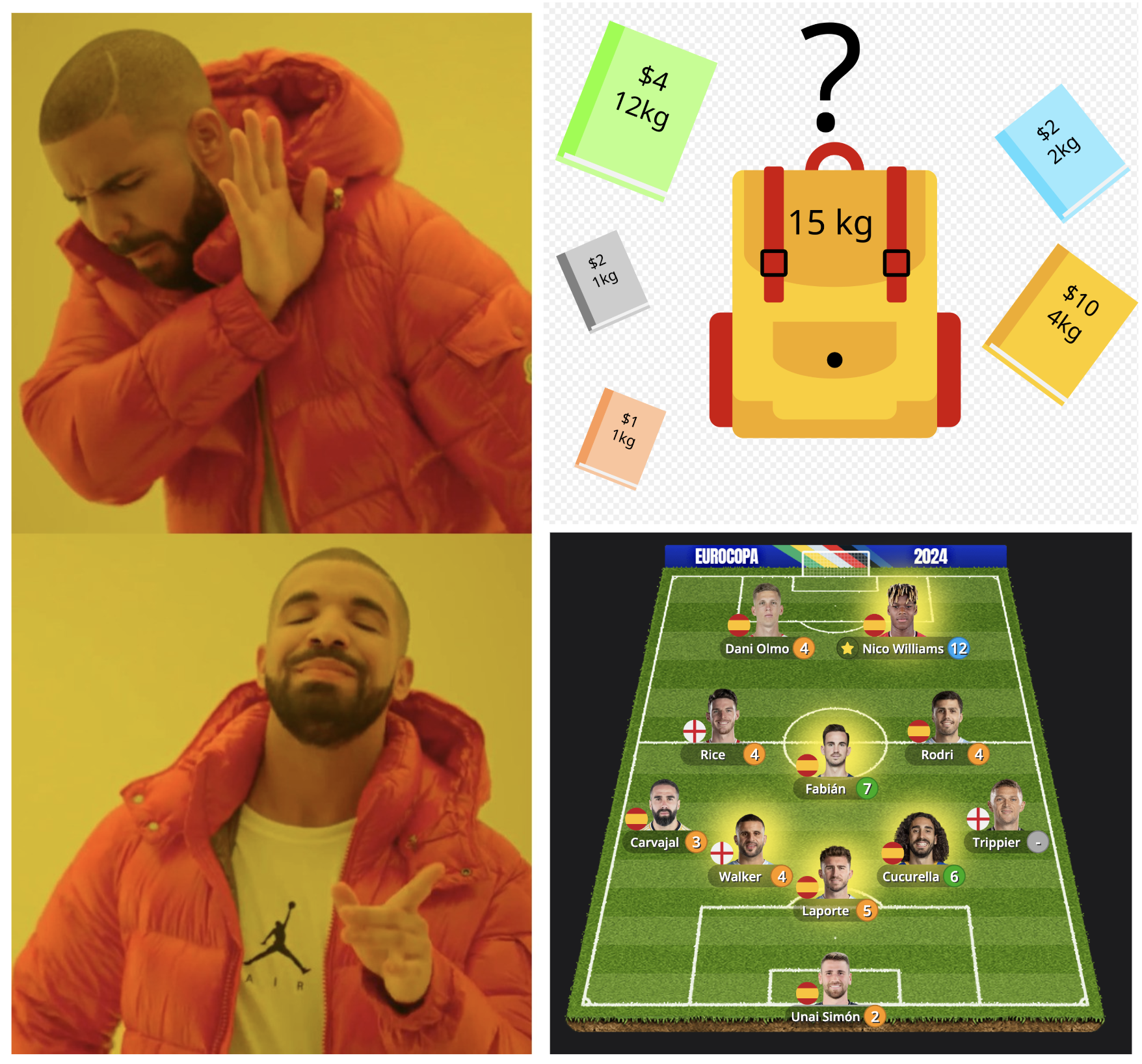
Drake Meme — Knapsack problem and fantasy sports are basically the same

For those unfamiliar with the knapsack problem here’s an example that may help you. Imagine you’re Indiana Jones, standing at the entrance of a treasure-filled temple. You’ve got a backpack with limited space, and you need to decide which artifacts to grab. Each artifact has its weight and value. Your objective is to maximize the value of the packed objects while fulfilling the space constraint. This scenario perfectly captures the essence of the knapsack problem. ⁵

In our fantasy league, we face a similar challenge. Instead of relics, we deal with players. And our goal is to build the most valuable team possible without exceeding our budget. It’s like trying to maximize the worth of Indy’s loot while staying within his backpack’s weight limit. So what’s better, to field Mbappe -which is expensive but usually plays very well- or to field Kante -which is cheaper but doesn’t get that many points?

Math

Getting more serious, the knapsack problem can be formulated as: given a set of $n$ items numbered from 1 up to $n$, each with a weight $w_i$ and a value $v_i$, along with a maximum weight capacity $W$, and $x_i$ being the number of copies of $i$,

\[\textrm{maximize} \sum v_i x_i\] \[\textrm{subject to} \sum w_i x_i < W\]

Here we restrict the problem to $x_i \in \{0, 1\}$, ie we can only select one copy of each element $i$. This simple problem is known to be NP-complete, which means no algorithm solves it fast (where fast means in polynomial time, whatever it means).

In our case, we have to choose $n=11$ players, each with a price $w_i$ and a score $v_i$ and the maximum budget of the team is $W=250$M. Easy peasy! We need to get the data and solve the corresponding knapsack problem and we’ll beat our friends. But…

It’s not that simple

The knapsack problem we just formulated is a simple one, but in our case, we have to deal with more complexity. In particular

We don’t have the data. The discussion until now has been purely theoretical, but if I want to beat my friends I need data from players (costs, positions, past performance, etc.).
Not all the lineups are valid. You can’t field 11 forwards and no goalkeeper so when solving the problem we need to take into account these constraints.
We don’t know the value of a player before the game. We only know the scores of the player in past games, but we can’t know how the player will perform in the next game ⁶.
Finally, once we have all the above problems fixed we need to solve the knapsack problem.

Let’s see how to solve these problems one by one.

Data

I’ve never been a front-end developer nor a scrapping expert, so my knowledge of how to get this data was very limited. But after playing a little bit with the developer console I realized that the web was calling always the same endpoint:

https://cf.biwenger.com/api/v2/competitions/<COMPETITION>/data?score=<SCORE>

where <COMPETITION> was the identifier of the competition (Biwenger hosts multiple competitions at the same time) and in our case was euro. And <SCORE> was the identifier of the scoring method used to evaluate players (Biwenger allows you to use multiple scoring options).

With this information, I managed to download all the player’s data, and it looked like

{
  "32142": {"id": 32142, "name": "Bardakcı", "slug": "a-bardakci", "teamID": 12, "position": 2, "price": 940000, "fantasyPrice": 7000000, "status": "ok", "priceIncrement": 190000, "playedHome": 2, "playedAway": 1, "fitness": [4, "sanctioned", 1, 5], "points": 10, "pointsHome": 6, "pointsAway": 4, "pointsLastSeason": null},
  "7470": {"id": 7470, "name": "Bastoni", "slug": "a-bastoni", "teamID": null, "position": 2, "price": 7480000, "fantasyPrice": 28000000, "status": "ok", "priceIncrement": 0, "playedHome": 1, "playedAway": 3, "fitness": [4, 4, 6, 14], "points": 28, "pointsHome": 14, "pointsAway": 14, "pointsLastSeason": 7},
  "32763": {"id": 32763, "name": "Buongiorno", "slug": "a-buongiorno", "teamID": null, "position": 2, "price": 1870000, "fantasyPrice": 17000000, "status": "ok", "priceIncrement": 0, "playedHome": 0, "playedAway": 0, "fitness": [null, null, null, null], "points": 0, "pointsHome": 0, "pointsAway": 0, "pointsLastSeason": null}
}

And then I parsed this information into a list of dataclasses

@dataclass(frozen=True)
class Player:
  player_id: int
  name: str
  position: int
  price: int
  status: str
  played_home: int
  played_away: int
  fitness: Tuple[int]
  points: int
  points_home: int
  points_away: int
  team_id: int

Player value

The next problem to solve was to predict player performance in the next game. The obvious solution for a data scientist like me was to use machine learning. But I didn’t. I just took the average score by the player during the last 5 games.

def player_value(player: Player):
  fitness = [value for value in player.fitness if isinstance(value, int)]
  if player.team_id is not None:
    return np.mean(fitness)
  else:
    return 0

Team constraints

The last thing we need to define are the constraints our team has to fulfill. We can implement these constraints using another dataclass

@dataclass(frozen=True)
class TeamConstraints:
  max_salary: int
  number_of_gk: Tuple[int, int] = (1, 1)
  number_of_df: Tuple[int, int] = (2, 5)
  number_of_mc: Tuple[int, int] = (2, 5)
  number_of_fw: Tuple[int, int] = (1, 5)
  max_n_players: int = 11

Solver

Now we have all the information we need, but how do we find the best team? How do we solve the knapsack fantasy problem?

To solve the problem we’ll use Google’s OR-tools, an open-source library for operations research. How does it work? Let’s see it step by step.

Define the solver

We’ll wrap everything in a custom class called Solver (yes, I know, I’m very creative), which looks like

class Solver:
    def __init__(
      self,
      player_value: Callable[[Player], float],
      player_cost: Callable[[Player], float],
      constraints: TeamConstraints,
      players: Dict[str, Player],
      ):
        self.player_value = player_value
        self.player_cost = player_cost
        self.players = players
        self.constraints = constraints

    def solve(self) -> Team:
      ... 

First of all, we need to initialize an OR-tools solver.

def solve(self) -> Team:
  solver = pywraplp.Solver(name="FantasyKnapsack", problem_type=pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
  ...

Now, with this solver, we can add constraints (budget, number of players, etc) and values to maximize (team score). But first, we need to define a couple of variables.

Selecting players and defining value

Let’s define now a list called take which will be 0 in position i if player i is not selected and 1 otherwise.

...
take = [solver.IntVar(0, 1, f"take_{p}") for p in self.players]
...

And now we define the value we want to maximize

...
value = solver.Sum(
 [self.player_value(p) * take[i] for i, p in enumerate(self.players.values())]
 )
solver.Maximize(value)
...

This means, we check for each player if it’s chosen or not (taken[i]) and we sum their values. Then we tell the solver we want to maximize this value, and the solver will build taken such that this value is maximized while fulfilling the constraints.

Constraints

Adding constraints to the solver is very easy. For example, to add the budget constraint we just need to do this:

...
budget = solver.Sum(
 [self.player_cost(p) * take[i] for i, p in enumerate(self.players.values())]
 )
solver.Add(budget <= self.constraints.max_salary)
...

As you can see the logic is very simple: sum the cost of each selected player and then add it as a constraint to the solver. We also need to define the number of players’ constraints, which is also very easy. In the following snippet, we can see how to add the constraint for the minimum and maximum number of goalkeepers

...
min_gk, max_gk = self.constraints.number_of_gk
number_of_gk = solver.Sum(
 [take[i] for i, p in enumerate(self.players.values()) if p.position == 1]
 )
solver.Add(number_of_gk >= min_gk)
solver.Add(number_of_gk <= max_gk)
...

And the logic is the same for defense, midfielders, and forwards.

Putting everything together

After defining the value to maximize and adding all the constraints we just need to ask the solver to find the optimal solution. You can check the full code below.

Full solver class

class Solver(BaseSolver):
  def __init__(
    self,
    player_value: Callable[[Player], float],
    player_cost: Callable[[Player], float],
    constraints: TeamConstraints,
    players: Dict[str, Player],
  ):
    self.player_value = player_value
    self.player_cost = player_cost
    self.players = players
    self.constraints = constraints

  def solve(self) -> Team:
    solver = pywraplp.Solver(
    "FantasyKnapsack", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING
    )
    take = [solver.IntVar(0, 1, f"take_{p}") for p in self.players]
    value = solver.Sum(
    [
    self.player_value(p) * take[i]
      for i, p in enumerate(self.players.values())
    ]
    )
    solver.Maximize(value)

    salary = solver.Sum(
      [self.player_cost(p) * take[i] for i, p in enumerate(self.players.values())]
    )

    solver.Add(salary <= self.constraints.max_salary)

    # number of players constraints
    min_pt, max_pt = self.constraints.range_pt
    number_of_gk = solver.Sum(
      take[i] for i, p in enumerate(self.players.values()) if p.position == 1
    )
    solver.Add(number_of_gk >= min_pt)
    solver.Add(number_of_gk <= max_pt)

    min_df, max_df = self.constraints.range_df
    number_of_df = solver.Sum(
      take[i] for i, p in enumerate(self.players.values()) if p.position == 2
    )
    solver.Add(number_of_df >= min_df)
    solver.Add(number_of_df <= max_df)

    min_mc, max_mc = self.constraints.range_mc
    number_of_mc = solver.Sum(
      take[i] for i, p in enumerate(self.players.values()) if p.position == 3
    )
    solver.Add(number_of_mc >= min_mc)
    solver.Add(number_of_mc <= max_mc)
    min_dl, max_dl = self.constraints.range_dl

    number_of_dl = solver.Sum(
      take[i] for i, p in enumerate(self.players.values()) if p.position == 4
    )
    solver.Add(number_of_dl >= min_dl)
    solver.Add(number_of_dl <= max_dl)

    number_of_players = solver.Sum(
      take[i] for i, p in enumerate(self.players.values())
    )
    solver.Add(number_of_players == self.constraints.max_n_players)

    # solving
    solver.Solve()
    assert solver.VerifySolution(1e-7, True)

    team = Team(
      player_value=self.player_value,
      player_cost=self.player_cost,
      players=[],
      constraints=self.constraints,
    )
    for i, p in enumerate(self.players.values()):
      if take[i].SolutionValue():
        team.add_player(p)

    team.check_constraints()
    return team

Results

Cool! We have a way to design fantasy teams, but how good is it? Is it better than a human player? Or have we just lost a lot of time implementing a solution that doesn’t work? To answer these questions I’ve participated in a couple of fantasy leagues from the Quarterfinals to the Final. I participated in two open leagues and one with my friends. Here are the results.

Friends results

| Stage         | Position  | Points | 1st Position Points  | Average Points |
|---------------|-----------|--------|----------------------|----------------|
| Quarterfinals | 6/9       | 73     | 86                   | 76             |
| Semifinal     | 3/9       | 55     | 66                   | 52             |
| Finals        | 6/9       | 55     | 73                   | 55             |
|---------------|-----------|--------|----------------------|----------------|
| Overall       | 4/9       | 191    | 214                  | 183            |

Open league results (Carrusel Deportivo)

| Stage         | Position  | Points | 1st Position Points  |
|---------------|-----------|--------|----------------------|
| Quarterfinals | 3038/6345 | 74     | 109                  |
| Semifinal     | 2299/6345 | 82     | 106                  |
| Final         | 1706/6345 | 91     | 102                  |

Open league results (Tomas Roncero)

| Stage         | Position  | Points  | 1st Position Points  |
|---------------|---------- |-------- |----------------------|
| Quarterfinals | 188/5837  | 62      | 84                   |
| Semifinal     | 200/5837  | 85      | 104                  |
| Final         | 570/5837  | 91      | 101                  |

Conclusions

From the above tables, it’s obvious that my approach hasn’t been enough to win and humiliate my friends. My teams scored the same as the average, which is not enough to win this type of league. Overall, after summing up all the points obtained, I finished the league 4th, which isn’t bad but it’s also not great.

On the other hand, I’m impressed by the results in the open leagues. In one of them, I did poorly (top 30-50%), but in the other one, the performance was very strong (top 3-9%). I don’t have the overall results since these leagues started at the beginning of the Euro while I only played for the last 3 stages.

One key takeaway is that while the algorithm didn’t dominate, it did manage to outperform a significant portion of human players in the larger leagues. This is encouraging, considering that many of these players likely have years of experience and intuition about fantasy football -or at least have watched more football than me.

Why did this solution do so poorly? Here are some things that can be fixed for future iterations

Score prediction was too naive. Using just the average of the last 5 games doesn’t capture form, injuries, or matchup difficulty. Using ML here would have helped a lot.
The algorithm tried to maximize the expected total score but didn’t take into account volatility. When doing this kind of portfolio optimization you want to maximize returns while keeping risk under a certain level.
It didn’t consider the schedule of matches, potentially selecting players who weren’t playing in a given round. In fact, for some games, I aligned players who weren’t playing for that stage, and sometimes this information is available before starting the game.
There was no consideration of player popularity or ownership percentages, which can be strategic in differentiating your team. I mean, for two players with the same expected score you might want to select the less popular one, to differentiate from other players.

I’m from Spain, so I’m speaking about the real and original football, the one that’s played with the foot and a ball, not with the hands and an egg. ↩
See point 54 in my 100 list. ↩
“A fantasy sport (also known less commonly as rotisserie or roto) is a game, often played using the Internet, where participants assemble imaginary or virtual teams composed of proxies of real players of a professional sport. These teams compete based on the statistical performance of those players in actual games.” Source. ↩
We’re playing using Biwenger’s platform. ↩
This is just an example, please don’t steal from treasure-filled temples. ↩
If you happen to know how a player will perform in the game next week, please call me and we’ll get very rich and not just win a stupid fantasy game. ↩