Bayesian A/B testing is not immune to peeking
Introduction
Over the last few months at RevenueCat I’ve been building a statistical framework to flag when an A/B test has reached statistical significance. I went through the usual literature, including Evan Miller’s posts. In his well known “How Not to Run an A/B Test” there’s a claim that with Bayesian experiment design you can stop at any time and still make valid inferences, and that you don’t need a fixed sample size to get a valid result. I’ve read this claim in other posts. The impression I got is that you can peek as often as you want, stop the moment the posterior clears a threshold (eg $P(A>B) > 0.95$), and you won’t inflate false positives. And this is not correct. If you’re an expert in Bayesian statistics this is probably obvious, but it wasn’t for me. So I decided to run some simulations to see what really happens, and I’m sharing the results here in case it can be useful for others.
Simulation and results
Picture the following scenario
- Baseline and variant have the same conversion rate $r$ (ie, no difference between them).
- Generate events following a Bernoulli distribution with parameter $r$, and update your prior using Bayes theorem (formulas here), starting from an uninformative prior, eg $\text{Beta}(1, 1)$.
- After every $N$ events, compute the posterior probability that one branch is better than the other (ie $P(B > A)$ or $P(A > B)$). If any of them exceeds $0.95$, declare a winner.
- Since baseline and variant have the same conversion rate $r$ declaring a winner is a false positive.
- Repeat for different peek intervals $N$ and conversion rates $r$.
I ran the simulations for different conversion rates $r \in \left(0.1\%, 1\%, 10\%\right)$ and peeking intervals $N \in \left(10^2, 10^3, 10^4, 10^5, 10^6\right)$ and the results are consistent. In the following plot, we see how the error rate increases as the $N$ decreases.
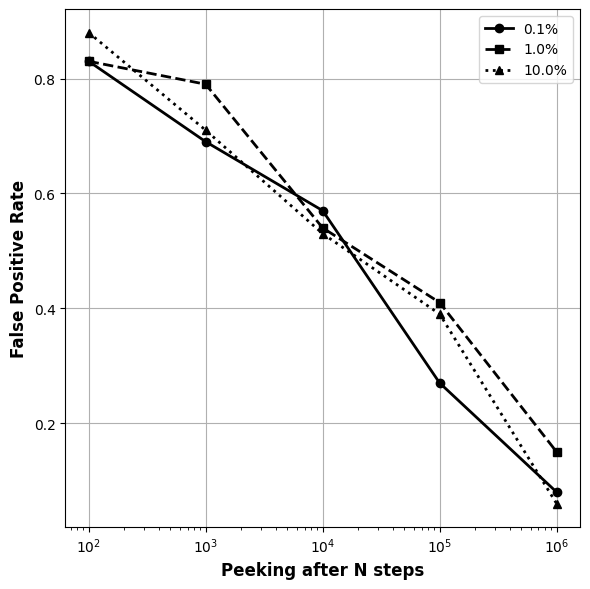
The plot show that as $N$ gets smaller, the error rate climbs. For example, if we peak after every $100$ observations the false positive rate increases to $80\%$. In other words, even when using a Bayesian approach, more frequent peeking increases the chance of calling a winner when there’s none.
The conclusion is then: Bayesian posteriors remain interpretable under continuous monitoring, but a fixed posterior threshold does not control false positives when you peek and stop on success
What can you actually do with Bayesian AB testing?
As we just saw, Bayesian AB testing is not immune to peeking. The more you peek the higher the false positive rate. But then, what advantage does it have over frequentist methods?
The key advantage is that results are interpretable at any sample size. This means you can monitor continuously and interpret $P(B > A)$ as the posterior probability that $B$ is better at the time you look. That interpretation is valid without a fixed sample size. However, if you want to control a frequentist error rate while peeking, a fixed $95\%$ posterior threshold will not do it.
What you cannot do is check daily and stop the moment you see favorable results. That’s optional stopping based on the outcome, and it inflates false positives just like in frequentist tests. The Bayesian advantage is that your posterior remains interpretable at any sample size. But “peek as often as you want and stop when you like” is a myth.